Vývoj těsných dvojhvězd
Vznik a raný vývoj dvojhvězd
Těsné dvojhvězdy jsou systémy hvězd, mezi jejichž složkami dochází k výměně hmoty, obíhají kolem společného hmotného středu po keplerovských drahách, ovlivňují se gravitačním působením (slapy), zářením, magnetickým polem a vzájemným přenosem hmoty. Většina všech hvězd se nachází v binárních systémech. Vznikají společně z jednoho plynného oblaku. Obě složky mají proto na počátku téměř stejné chemické složení. Malé procento binárních hvězd může také vzniknout po přiblížení dvou osamocených hvězd vzájemným zachycením nebo výměnou mezi osamocenou hvězdou a dvojhvězdou.
 |  |
Dvojhvězda | Přetok hmoty |
Pozorování dvojhvězd je důležité z toho důvodu, že jen v takovýchto systémech je možné spolehlivě změřit hmotnost jednotlivých složek. Pokud známe jejich vzájemnou oběžnou dobu a velkou poloosu jejich dráhy, můžeme podle vzorce (M1+M2)P2=a3, kde M1 a M2 jsou hmotnosti složek, P je jejich oběžná doba a a velká poloosa jejich dráhy) zjistit součet jejich hmotností. Poměr hmotností jednotlivých složek můžeme pak zjistit z poměru jejich vzdáleností od hmotného středu soustavy nebo z poměrů jejich oběžných rychlostí. Další důvod významu dvojhvězd je ten, že některé jevy mohou vznikat právě jen v systémech dvojhvězd (novy, supernovy I. typu apod.).
Členové dvojhvězd a vícenásobných hvězdných soustav tvoří vázaný systém už od momentu svého vzniku. Hvězdy v násobných systémech vznikly společně. Poměrně vysoké procento hvězd vázaných ve dvojhvězdách (až 70 %) naznačuje, že vznik hvězd ve dvojhvězdách je výhodnější, než vznik samostatných hvězd. Vysvětlujeme si to tak, že dvojhvězdy elegantně odstraňují jednu z hlavních překážek, které stojí v cestě formování nových hvězd – kam s přebytečným momentem hybnosti. Ve dvojhvězdách se moment hybnosti, který by jinak zrodu hvězdy bránil, uloží do orbitálního pohybu složek. Členové dvojhvězdy jsou tak hvězdná dvojčata, hvězdy jež se zrodily současně, mají stejné stáří (vzácně mohou dvojhvězdy vzniknout i zachycením, vždy však u toho musí asistovat třetí těleso, které se v při přiblížení prvých dvou hvězd musí nacházet poblíž nich ve vhodném místě, aby na sebe převzala kinetickou energii a hybnost. V hustých hvězdokupách to nemusí být tak výlučný jev). Dál je nepochybné, že se zformovaly ve stejné části zárodečného oblaku, mají tedy totéž počáteční chemické složení. Pozorováním systémů, zejména zákrytových dvojhvězd, získáváme spolehlivé informace o hmotnostech, absolutních rozměrech, efektivních teplotách a vzdálenostech jednotlivých hvězd. To z nich činí mimořádně vhodné kandidáty pro komplexní testování teorie hvězdné stavby a hvězdného vývoje. Nicméně při interpretaci vývojového statutu některých zákrytových dvojhvězd narazili astronomové na výrazné obtíže. Týká se to i první z objevených zákrytových dvojhvězd, hvězdy β Persei, známější jako Algol.
Paradox Algolu
Algol je zákrytovou dvojhvězdou sestávající ze dvou různých hvězd – ze žhavé hvězdy hlavní posloupnosti o hmotnosti pěti Sluncí a vývojově pokročilejšího podobra s hmotností několikanásobně menší. Zde je právě onen paradox: pokud jde skutečně o hvězdy stejně staré, měla by být vývojově pokročilejší ta hmotnější hvězda, která ve shodě s teorií hvězdné stavby rychleji spotřebovává své zásoby jaderného paliva. Zajímavé vysvětlení tohoto paradoxu přinesla hypotéza Johna Crawforda (1955) a Freda Hoyla, která je mezi astronomy známa pod názvem: „pes požírá psa”. Podle jejího scénáře se zpočátku obě složky hvězdného páru vyvíjejí tak, jak jim to předepisuje vývojová teorie vybudovaná pro osamocené hvězdy. Hmotnější složka žije rychleji a po čase, kdy v jádru vyčerpá své zásoby vodíkového paliva, se začne rozpínat a měnit se v rozměrného obra. Zatímco osamělá hvězda se přitom může nafukovat do libosti, složka v těsné dvojhvězdě nemá pro takové nadýmání dostatek místa. Ve svém rozpínání je omezena jistým hraničním objemem, zvaným Rocheův lalok. Hvězda vyplňující lalok je vlivem oběhu kolem hmotného středu soustavy i vlivem přitažlivosti druhé složky deformována do podoby zploštělé kapky se špičkou obrácenou k druhé složce. Motor hvězdného vývoje umístěný v centru hvězdy se na to neohlíží, pracuje dál a nutí hvězdu kynout. Ze špičky kapkovitě protažené hvězdy začne prýštit proud hvězdného materiálu směrem k druhé, vývojově opožděné složce. Nadýmající se hvězda je doslova vymačkávána na druhou hvězdu. Vývoj pokračuje překotným tempem (odtok látky z hvězdy vede k tepelné nestabilitě vnějších vrstev projevující se na Kelvinově – Helmholtzově časové škále, což vlastní proces přenosu ještě dále urychluje). Na druhou složku přeteče až 85 % její hmoty. Poměry hmotností v soustavě se převrátí – původně primární složka se stane málo hmotným obrem, přičemž ta méně hmotná hvězda převezme její vedoucí postavení v systému. Tento stav se pak na nějakou dobu udrží. A právě to je ten obrázek, který nám soustava Algolu dnes skýtá. Pro vysvětlení paradoxu Algolu má rozhodující roli Rocheova plocha, popisem jejích vlastností se budeme zabývat v dalších odstavcích.
Rocheovy plocha a klasifikace těsných dvojhvězd
Ekvipotenciální plochy, čili plochy, jež jsou množinou všech bodů o zvoleném potenciálu, mají ve stavbě kosmických těles velký význam. Pohybuje-li se bod po ekvipotenciální ploše, nekoná práci, neboť se pohyb děje kolmo k působící síle. Jsou-li objekty, udržované pohromadě vlastní gravitací, složeny z plastického materiálu (může se pohybovat), pak v nich plochy se stejnou hustotou musí v rovnovážném stavu zaujímat tvar ekvipotenciálních ploch. Vzhled ekvipotenciálních plochy v případě dvojhvězdy je poměrně komplikovaný, a to i pro ten nejjednodušší myslitelný případ, kde obě hvězdy bereme za hmotné body, které kolem společného těžiště krouží po kruhových drahách ve stálé vzdálenosti a úhlovou rychlostí ω, přičemž rotace obou hvězd je vázaná (perioda rotace = oběžná doba). Potenciál takovéto soustavy v korotující soustavě (neinerciální) spojené s oběma hvězdami v bodě {x,y,z}:Φ(x,y,z) pak sestává ze součtu gravitačních potenciálů vzhledem k oběma hvězdám o hmotnostech M1 a M2 a členu odpovídajícímu fiktivnímu potenciálu odstředivé síly:
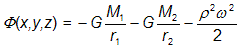 ,
,kde ρ je vzdálenost vybraného bodu od normály k orbitální rovině procházející těžištěm, a je vzájemná vzdálenost složek, r1 a r2 jsou vzdálenosti zvoleného bodu od prvního a druhého tělesa.
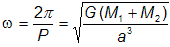 .
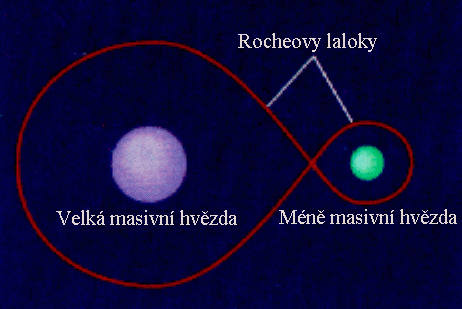
. Řez ekvipotenciálními plochami v rovině oběhu systému je na obrázku. Zvláštní význam zde má vnitřní ekvipotenciála, nazývaná Rocheova plocha nebo též kritická plocha. Tato plocha v prostoru vymezuje dva Rocheovy laloky, které se vzájemně dotýkají v tzv. bodě L1 čili v prvním Lagrangeově libračním bodě.
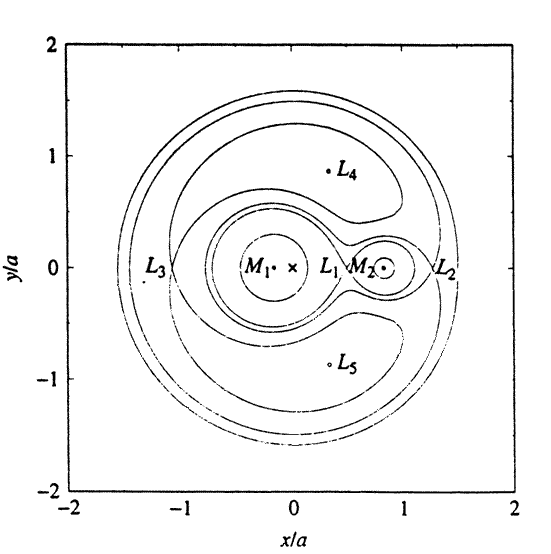
Geometrie Rocheových ekvipotenciál dle očekávání závisí pouze na poměru hmotností obou složek. Poněkud nečekaný je ovšem výsledek, že úhel, pod nímž se dotýkají špičky kritického Rocheova laloku v bodu L1 prakticky nezávisí ani na tom poměru a činí asi 115°, což je konečně patrno i z tabulek v často citované práci Plavce a Kratochvíla (Harmance) z roku (1964). Z údajů zde uvedených byl odvozen i užitečný aproximativní vztah pro vzdálenost Lagrangeova bodu L1 od středu první složky l1:
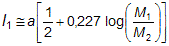 .
. Ačkoli Rocheův lalok nemá kulový tvar, lze definovat jistý poloměr Rocheova laloku RL, který odpovídá poloměru koule o jeho objemu. Aproximační vztah odvodili Icko Iben a Alexandr V. Tutukov (1984):
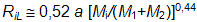 .
. Částice nacházející se uvnitř každého z laloků podléhají převážně gravitaci pouze jedné ze složek, částice vně laloků patří oběma složkám a vykonávají dosti komplikovaný pohyb (pokud je trajektorie dvojhvězdy výstředná, pak se situace poněkud komplikuje, nicméně právě při silné slapové interakci mezi složkami dochází k poklesu výstřednosti a přechodu hvězd na víceméně kruhové trajektorie). Složka dvojhvězdy, na rozdíl od samostatné hvězdy, nemá tedy k dispozici neomezený prostor. Začne-li se během vývoje jedna ze složek rychleji rozpínat, pak postupně zaplňuje stále vyšší ekvipotenciální plochy, dokud její povrch nenarazí na Rocheovu plochu. V té chvíli se povrchové vrstvy hvězdy stávají společným vlastnictvím obou složek. Látka začne singulárním bodem přetékat do prostoru druhého z Rocheových laloků a může se časem dostat až na druhou ze složek. Takto dochází v těsných dvojhvězdách k přenosu látky mezi složkami. Během vývoje soustavy k takovémuto přenosu látky může dojít i několikrát a může se při něm přenést podstatná část hmoty soustavy.
Těsné dvojhvězdy jsou takové podvojné systémy, kde v průběhu vývoje dojde k tomu, že alespoň jedna ze složek vyplní svůj Rocheův lalok a dojde tak k přenosu látky směrem k druhé složce. Při běžných hmotnostech složek můžeme mezi těsné dvojhvězdy řadit všechny, jejichž perioda je kratší než několik desítek dní. Vzhledem k tomu, že se toto týká většiny dvojhvězd, je zřejmé, že ve většině pozorovaných dvojhvězd buď již došlo k přenosu látky, nebo k němu dříve či později dojde. V roce 1955 zavedl astronom českého původu Zdeněk Kopal (1914-95) pro těsné dvojhvězdy velmi důležitou a dodnes všeobecně používanou vývojovou klasifikaci dvojhvězd podle jejich vztahu k Rocheově ploše.

- Oddělené soustavy (detached systems), jsou ty, v nichž jsou povrchy obou složek uvnitř Rocheovy plochy.
- Polodotykové soustavy (semidetached systems), jsou takové, kde jedna ze složek vyplňuje svůj Rocheův lalok. V těchto soustavách dochází přes bod L1 k přenosu látky směrem od dotykové složky na složku oddělenou. Příkladem mohou být těsné dvojhvězdy typu Algol.
- Dotykové soustavy (contact systems) – zde své Rocheovy laloky vyplňují obě složky. Tyto složky mají pak třeba společnou atmosféru (případ zákrytových dvojhvězd typu W Ursae Majoris).
Vývojový scénář. Konzervativní přetok látky
Pro většinu těsných dvojhvězd platí v hrubých rysech tento základní vývojový scénář:
- Obě hvězdy, pokud se nacházejí na hlavní posloupnosti, leží uvnitř svých Rocheových laloků, a tvoří tak oddělené systémy. Hvězdy mají týž tvar jako hvězdy osamocené a vyvíjejí stejně jako ony.
- V soustavě se rychleji vyvíjí hmotnější (primární) složka systému. Když v jejím centru poklesne obsah vodíku v jádru pod 5 %, dojde k poměrně rychlé expanzi svrchních vrstev hvězdy, při níž se poloměr osamocené hvězdy zvětšuje mnohonásobně. V těsné dvojhvězdě však prostor není neomezený, v jistém okamžiku se stane, že hvězda vyplní svůj Rocheův lalok. Vzniká tak polodotyková soustava.
- Bodem L1 začne z primární složky prýštit na sekundární složku látka. Ta přijímá nejen tuto látku, ale i moment hybnosti, který se nutně též přenáší. Oběžná perioda klesá. Dochází k rychlému vývoji, na jehož závěru si obě složky vymění své role, primární složka se stane složkou sekundární a naopak.
- Po výměně rolí v systému se nyní již sekundární složka vyvíjí tak, jak tomu odpovídá stav jejího nitra. To je natolik husté, a tudíž samostatné, že se jej děje probíhající ve svrchních vrstvách hvězdy takřka nijak nedotknou. To znamená, že i když je faktická hmotnost hvězdy stále zkracována přenosem, hvězda se vyvíjí zhruba tak, jako by neustále měla svou počáteční hmotnost. Sekundární složka tak bude mít i nadále před složkou primární ve vývoji náskok. Vzhledem k tomu, že vývoj hvězdného nitra vede k neustálému rozpínání obalu hvězdy, bude přenos látky pokračovat, byť v pomalejším tempu, perioda soustavy by přitom měla opět pozvolna růst. Ve fázi tohoto pomalého přetoku látky nacházíme řadu zákrytových dvojhvězd, kde se běžně setkáváme s tím, že hmotnější a jasnější složka je hvězdou hlavní posloupnosti pod Rocheovou plochou, zatímco sekundární složkou bývá vývojově pokročilý podobr vyplňující svůj Rocheův lalok.
Hlavní rysy procesu přenosu látky mezi složkami si lze přiblížit pomocí tzv. konzervativního přetoku látky, při němž během přenosu látky žádná hmota ze systému neunikne do prostoru. V soustavě nechť je dále všechna látka vázána na jednu či druhou složku, takže pak platí,M1 + M2 = M = konst., totéž bude platit i momentech hybnosti:L1 + L2 = L = konst., složky nechť stále obíhají po kruhových trajektoriích. Vypočítejme si nyní, jak bude za těchto okolností záviset vzdálenost složek a a jejich oběžná perioda P na okamžitých hmotnostech složek, přičemž a1 a a2 jsou vzdálenosti první a druhé složky od těžiště a x je parametr, který charakterizuje rozdělení hmoty systému mezi složkami:
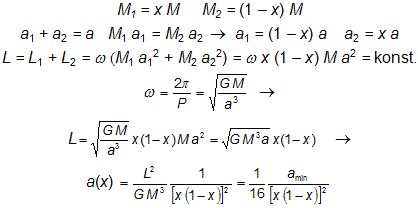 .
. Závislost vzdálenosti složek a(x) na parametru x je reprezentována funkcí, která má tvar písmene U. Je symetrická vůči vertikále: x = 0,5, v bodech x = 0 a x = 1 roste nade všechny meze. To nám dává velmi důležitou informaci o chování systému při přenosu látky. Jestliže primární ze složek naplní svůj lalok a začne přetékat na druhou složku, pak se počáteční hodnota parametru x0 (0,5<x0<1) bude zmenšovat. Znamená to, že obě složky se k sobě začnou přibližovat, a to až na minimální vzdálenost amin.
 Konzervativní přetok látky mezi dvěma hvězdami
Konzervativní přetok látky mezi dvěma hvězdamiObjem Rocheova laloku stále ještě primární složky se začne zmenšovat, a to hned ze dvou příčin:
1) zmenšuje se poměr hmotnosti obou složek,
2) složky se v prostoru k sobě přibližují. Hmota primární složky uložená v laloku je tak doslova vymačkávána na druhou složku, celý proces je natolik rychlý (snad až 0,01 /rok), že je jen malá šance některý z dvojhvězdných systémů v této fázi přenosu přistihnout. Velmi brzy dojde k tomu, že se x zmenší pod 0,5, role složek v soustavě se převrátí – sekundární složka se stane primární a naopak. Po tomto aktu se vývoj viditelně zvolní, neboť při dalším odtoku látky se vzdálenosti složek již budou zvětšovat a objem Rocheova laloku nyní již sekundární složky mírně poroste. Tempo vývoje pak bude dáno tempem dějů v nitru hvězdy. Obdobné je i chování oběžné periody systému v průběhu přenosu látky. Jak plyne z 3. Keplerova zákona pro případ kruhových drah:
/rok), že je jen malá šance některý z dvojhvězdných systémů v této fázi přenosu přistihnout. Velmi brzy dojde k tomu, že se x zmenší pod 0,5, role složek v soustavě se převrátí – sekundární složka se stane primární a naopak. Po tomto aktu se vývoj viditelně zvolní, neboť při dalším odtoku látky se vzdálenosti složek již budou zvětšovat a objem Rocheova laloku nyní již sekundární složky mírně poroste. Tempo vývoje pak bude dáno tempem dějů v nitru hvězdy. Obdobné je i chování oběžné periody systému v průběhu přenosu látky. Jak plyne z 3. Keplerova zákona pro případ kruhových drah: .
. Perioda soustavy se během rychlé fáze přetoku snižuje do svého minima - Pmin, po výměně rolí složek pak opět roste.
Pokud nejsou splněny podmínky konzervativního přetoku, pak velmi silně záleží na tom, jaký díl momentu hybnosti si sebou látka unikající ze systému odnáší. Výpočty jsou ovšem příslušně složitější než ty, které byly naznačeny výše. - Během rychlého a později pomalého přetoku látky může původně hmotnější hvězda předat druhé složce až 85 % své hmoty, vesměs přitom jde o kvalitní, na vodík bohatý materiál, který nebyl dotčen předchozím jaderným vývojem hvězdy. Přetok látky z jedné složky na druhou nemusí vždy probíhat bezprostředně. Plynný proud látky si sebou nese svůj moment hybnosti, což vede k tomu, že nesměřuje přímo na druhou složku, ale poněkud stranou. Pokud není hmotu přijímající složka dostatečně rozměrná, pak se kolem ní nejprve vytvoří poměrně tenký disk ležící v orbitální rovině soustavy. Vlivem tření v disku (zejména turbulentního) se moment hybnosti vnitřních částí disku přenáší do vnějších oblastí, což umožňuje vnitřním částicím, aby se po spirále postupně snesly na povrch hmotu přijímající složky. Zvyšování hmotnosti hvězdy na hlavní posloupnosti vede k nárůstu vnitřní teploty, tím ke snížení opacity a zvýšení koncentrace nosičů tepla (fotonů) a rychlosti přenosu energie, čili k nárůstu výkonu hvězdy. Vývoj hvězdy se tak patřičně zrychlí, náskok hmotu darující složky však nedožene.
- Sekundární složka při pomalém přetoku postupně přichází o takřka veškerý svůj obal. Její další vývoj pak závisí na její počáteční hmotnosti:
- Je-li počáteční hmotnost hvězdy menší než 3 Slunce, pak vznikne heliová hvězda o hmotnosti menší než 0,45 Slunce. Ta elektronově zdegeneruje dříve, než se v ní vytvoří teplota dostatečná k zapálení heliových reakcí. Z hvězdy se pak časem vyvine elektronově degenerovaný heliový bílý trpaslík.
- Je-li počáteční hmotnost hvězdy větší než 3 Slunce, pak se při smrštění hvězdy heliové reakce přece jen vznítí a hvězda se na 105 až 106 let stává horkou hvězdou hlavní heliové posloupnosti. Pro ty je charakteristický silný hvězdný vítr. Brzy ve hvězdě pokročí degenerace natolik, že se z ní stane uhlíko-kyslíkový bílý trpaslík. Pokud na něj bude přetékat látka z druhé složky, pak může cyklicky vybuchovat jako nova, eventuálně se může stát supernovou typu Ia.
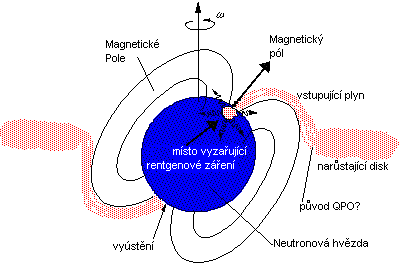
- Je-li hmotnost větší než 15 Sluncí, pak je vývoj podobný, jen s tím rozdílem, že v nitru hvězdy, které je díky své vyšší teplotě a nižší hustotě více vzdáleno elektronové degeneraci, se postupně zapalují stále další a další jaderné reakce. Vše končí u reakcí, které produkují železo. Pakliže hmotnost elektronově degenerovaného železného jádra překročí 1,4 Slunce, tento vnitřek se zhroutí v neutronovou hvězdu, případně černou díru. Hvězda vzplane jako supernova typu II nebo Ib, zůstává po ní neutronová hvězda či černá díra. Dvojice hvězd, v nichž sekundární složku tvoří takovýto objekt, běžně pozorujeme. Jde o tzv. rentgenové dvojhvězdy, burstery apod., kde z primární složky přitéká látka ke zhroucenému objektu, což dává vznik měkkému gama záření.
- Další vývoj může být velmi rozmanitý, protože nyní se do aktivní role dostává primární složka. Když ta vyplní svůj lalok, začne látka z této hvězdy přetékat směrem ke zhroucené sekundární složce (bílý trpaslík, neutronová hvězda, černá díra - vzhledem k tomu, že tyto hvězdy jsou lineárně nesmírně malé, látka na ně přímo nedopadá, vždy se kolem nich vytváří akreční disk. Postupný pád látky na zhroucenou složku je doprovázen uvolňováním značné energie, která vlastně reguluje příliv nové hmoty na zhroucenou složku). V důsledku ztráty látky se může podvojný systém i úplně rozpadnout nebo v něm nakonec najdeme dva bílé trpaslíky, či jiné kombinace objektů v závěrečném stádiu vývoje.
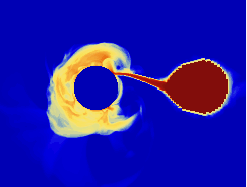
 3D počítačový model konzervativního toku látky mezi hvězdami
3D počítačový model konzervativního toku látky mezi hvězdami
Neutronové hvězdy a černé díry v interagujících dvojhvězdách
Neutronové hvězdy o sobě dávají vědět, pokud jsou dostatečně mladé – tehdy září jako radiové pulsary. Starší hvězdy, které již tak rychle nerotují, lze odhalit jen obtížně. Výjimkou jsou ty neutronové hvězdy, které jsou členkami těsných dvojhvězd, v nichž dochází k přenosu látky. Tato látka dopadá na povrch neutronové hvězdy, čímž se uvolňuje velké množství gravitační energie, jež se pak mění v energii neuspořádaného pohybu částic. Akreovaný plyn se zahřívá na teplotu milionů kelvinů a září převážně v rentgenovém oboru spektra. Takovým soustavám se říká rentgenové dvojhvězdy. Rozličné konfigurace zhroucené složky a její průvodkyně v podvojné soustavě dávají bezpočet variant neobvyklých projevů neutronových hvězd v podobě rentgenových pulsarů, zábleskových zdrojů, přechodných rentgenových zdrojů, rentgenových nov, zdrojů záblesků měkkého i tvrdého záření gama. Dosti podobně se projevují i černé díry nacházející se v interagující dvojhvězdě. Zde přetéká část hmoty normální složky na zhroucený objekt, a to buď prostřednictvím hvězdného větru nebo přímým přetokem v případě, kdy objem vyvíjející se hvězdy vyplní tzv. Rocheův lalok. Zvláště v tomto případě s sebou nese přetékající látka značný moment hybnosti. Podle zákona zachování momentu hybnosti nepadá látka přímo na černou díru, ale vytváří kolem ní mohutný plochý rotující disk. Vlivem tření se v akrečním disku přenáší moment hybnosti směrem od hvězdy, což umožňuje vnitřním částicím disku sestupovat stále níže k černé díře, dokud se nedostanou na nestabilní trajektorie, po nichž nezadržitelně padají do jícnu černé díry. Při těchto procesech se uvolňuje obrovské množství energie, která nahřívá vnitřní části akrečního disku na teploty řádově milionů kelvinů. Látka má podobu vysoce ionizovaného plazmatu, kde důležitou roli hraje magnetické pole. Vnitřek akrečního disku září jako rentgenový zdroj.