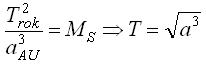Planetka
2014 WH460
| (692451) 2014 WH460 | |
|---|---|
| Předběžné označení | 2014 WH460 |
| Katalogové číslo | 692451 |
| Název | 2014 WH460 |
| Objevena | |
| Kdy | 18. listopadu 2014* |
| Kde | Mount Lemmon |
| Kým | Mount Lemmon Survey |
| Elementy dráhy (Ekvinokcium J2000,0) | |
| Epocha | 21. listopadu 2025 0:00:00 UTC |
| Velká poloosa dráhy – a | 3,0787 au – 460 567 144 km |
| Excentricita – e | 0,1251 |
| Střední denní pohyb – n | 0,1825°/den |
| Sklon dráhy k ekliptice – i | 1,1810° |
| Délka vzestupného uzlu – Ω | 26,4261° |
| Argument šířky perihelu – ω | 157,8093° |
| Střední anomálie – M | 268,9509° |
| Další údaje | |
| Absolutní hvězdná velikost – H | 17,08 mag |
| Fázový parametr – G | 0,15 |
| Počet pozorování*) | 95 |
| Počet opozic*) | 12 |
| Pozorována v letech*) | 2000–2024 |
| Poslední pozorování*) | 27. září 2024 |
| Typ planetky | planetka v hlavním pásu |
| Odvozené údaje z elementů dráhy a dalších údajů | |
| Vzdálenost v přísluní – q | 2,694 au – 402 945 000 km |
| Vzdálenost v odsluní – Q | 3,464 au – 518 189 000 km |
| Oběžná doba – T | 5,402 roků – 1 973,1 dnů |
| Vektor P [x] Vektor P [y] Vektor P [z] Vektor Q [x] Vektor Q [y] Vektor Q [z] | −0,9972 −0,0709 −0,0223 0,0738 −0,9072 −0,4141 |
| Průchody přísluním (v JD) | 8. listopadu 2021 (2 459 527), 4. dubna 2027 (2 461 501), 28. srpna 2032 (2 463 474) |
| Průchody odsluním (v JD) | 22. července 2024 (2 460 514), 16. prosince 2029 (2 462 487), 12. května 2035 (2 464 460) |
| Tisserandův parametr – TJ (vztažený k Jupiteru) | 3,2 |
| Největší přiblížení k Zemi**) | 24. března 2027 (1,70 au) |
| Nejjasnější ze Země**) | 22. března 2027 (20,4 mag) |
| Nejdále od Země**) | 30. března 2046 (4,46 au) |
| Nejméně jasná ze Země**) | 23. května 2035 (23,6 mag) |
**) hodnoty pro největší/nejmenší přiblížení a nejnižší/nejvyšší pozorovanou hvězdnou velikost
jsou spočítány pro období od 3. února 2026 do 31. prosince 2050 s intervalem 1 den.
Poloha planetky ve Sluneční soustavě
Na obrázku je v základním nastavení znázorněna aktuální poloha planetky ve Sluneční soustavě v rovině ekliptiky. Měřítko je zvoleno automaticky podle vzdálenosti planetky v odsluní (aféliu) tak, aby se celá trajektorie planetky vykreslila a optimálně vyplnila plochu obrázku. Dle měřítka, které lze změnit z vybraných hodnot, je vykreslena i poloha (včetně trajektorií) některých planet Sluneční soustavy. Barva čáry trajektorie naznačuje, zda se planetka nachází nad rovinou ekliptiky (modře) nebo pod ní (červeně).
Polohu těles ve Sluneční soustavě lze vykreslit i pro jiné datum (nebo "dnes"), které se zadává pomocí formuláře pod obrázkem. Lze zadat datum ±50 let od dnešního dne. Obrázek se průběžně aktualizuje po zadání hodnot. Po spuštění animace (zpětně, dopředu) se poloha těles pravidelně mění v intervalu den, měsíc nebo rok (uživatelská volba). Rychlost animace je závislá na době potřebné pro vygenerování obrázku (řádově 0,5-0,8 s).
Dráhové elementy kosmických těles ve Sluneční soustavě se vlivem gravitace Jupitera a Saturna neustále mění. Pro Slunce (potažmo Zemi) a planety jsou platné pro delší časové období. Nicméně pro planetky je obtížné jejich určení, neboť je závislé na mnoha faktorech - zejména na přesnosti, jakou požadujeme. Planetka se může pohybovat po zhruba stále stejné trajektorii po několik oběhů, nicméně při průletu poblíž Jupiteru se může její trajektorie radikálně změnit. Je složité toto obecně určit. Chyba narůstá s časem.
U přísluní a odsluní se zobrazuje vzdálenost objektu od Slunce, rychlost a odhad efektivní teploty rovnovážného záření planetky, přičemž je uvažováno Bondovo albedo A = 0,09. Pro výpočet efektivní teploty je použit Stefanův-Boltzmannův zákon a planetku modelujeme jako kouli v termodynamické rovnováze. Absorpce záření od Slunce planetkou je plochou průřezu, kdežto emise povrchem koule.
Výpočet pozorované hvězdné velikosti …
K výpočtu pozorované hvězdné velikosti planetky je použit tzv. HG-systém, kde H označuje absolutní hvězdnou velikost planetky, což je pozorovaná hvězdná velikost planetky ve vzdálenosti 1 au od pozorovatele a 1 au od Slunce při nulovém fázovém úhlu, a G je fázový parametr, který souvisí s efektem zjasnění v opozici, kdy se jasnost planetky zvýší zhruba o 0,3 mag. Hodnota G není známa pro mnoho planetek, pro ostatní se používá hodnota 0,15. Fázový úhel α je definován jako úhel mezi směrem k pozorovateli a směrem ke Slunci, měřený od středu planetky. Je nulový, pokud se planetka nachází v opozici.
Průměrnou pozorovanou hvězdnou velikost planetky můžeme vyjádřit jako
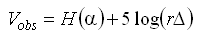 ,
,
kde r je vzdálenost planetky od Slunce, Δ je její vzdálenost od Země a H(α) je redukovaná hvězdná velikost. Její velikost vypočteme pomocí fázového zákona
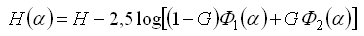 ,
,
přičemž fázový parametr G slouží jako váhový parametr dvou fázových funkcí Φ1(α) a Φ2(α). Fázovou funkci vyjádříme
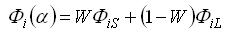 , i = 1, 2,
, i = 1, 2,
kde
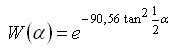 ,
,
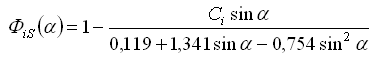 ,
,
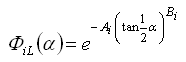 , i = 1, 2
, i = 1, 2
a parametry A1 = 3,332; A2 = 1,862; B1 = 0,631; B2 = 1,218; C1 = 0,986 a C2 = 0,238.
Výpočet efektivní teploty planetky …
Sálání (záření) je přirozená vlastnost těles, souvisí se změnami vnitřní energie tělesa. Těleso vydává záření ve formě elektromagnetických vln do prostoru. Dopadne-li toto záření na jiné těleso, je částečně pohlceno, část se odráží a část prochází tělesem. Pohltivost a odrazivost záření u tělesa závisí na jakosti a barvě povrchu. Pro přenos tepla zářením není potřeba žádné hmotné prostředí, jde o elektromagnetické vlnění.
Pro výkon záření černého tělesa P platí upravený Stefanův-Boltzmannův zákon
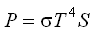
kde S je obsah plochy povrchu tělesa v m2, T je teplota tělesa v kelvinech a σ je Stefanova-Boltzmannova konstanta.
Uvažujeme, že planetka i fotosféra Slunce vysílají i přijímají záření jako černá tělesa. Označíme teplotu fotosféry Slunce T (5 780 K), poloměr Slunce R (696 tisíc km), poloměr planetky r, teplotu povrchu planetky Tp a vzdálenost mezi Sluncem a planetkou d.
Na planetku dopadá část tepelného záření vyzařovaného fotosférou Slunce. Tuto část vypočítáme jako poměr průřezu planetky a povrchu koule ve vzdálenosti planetky, tzn.
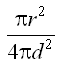
Tepelný výkon přijímaný planetkou od fotosféry Slunce je
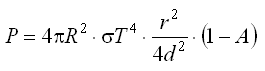 ,
,
kde A je Bondovo albedo, uvažované na hodnotě 0,07. Albedo (míra odrazivosti) planetek se obecně pohybuje v rozmezí 0,02 až 0,5. Nízké albedo (0,02 až 0,07) má 78 % známých planetek hlavního pásu větších než 25 km. Střední albedo (0,08 až 0,12) mají zhruba 4 % planetek. Mírné albedo (0,13 až 0,28) má 18 % planetek.
Tento tepelný výkon vyzařuje povrch planetky, přičemž uvažujeme vlivem rychlého otáčení a dobré tepelné vodivosti rovnoměrné rozložení teploty Tp povrchu planetky
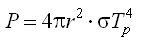 .
.
Z rovnosti výkonů dostaneme po úpravě
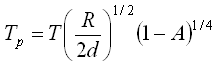 .
.
Modelování vyjádření problematiky výpočtu teploty planetky nemusí plně odpovídat realitě. Planetky nejsou sférická tělesa, rotují velmi různě, i samotný jejich povrch může mít v různých místech odlišné albedo apod. I přesto nám může vypočítaná hodnota přinést představu o teplotě v dané vzdálenosti od Slunce.
Ověření Keplerových zákonů …
- První Keplerův zákon
"Planety obíhají kolem Slunce po eliptických drahách, v jejichž jednom společném ohnisku je Slunce."
Poloha Slunce je vyznačena žlutým symbolickým obrázkem, černý čtvereček znázorňuje polohu prvního ohniska F1.
Druhé ohnisko F2 je zobrazeno modrým čtverečkem. Červený čtvereček vyznačuje střed elipsy.
Bod na eliptické trajektorii, v němž je planeta nejblíže Slunci, se nazývá přísluní, bod, v němž je
planeta nejdále od Slunce, se nazývá odsluní. Spojnice obou se nazývá přímka apsid.
- Druhý Keplerův zákon
"Obsahy ploch opsaných průvodičem planety (spojnice planety a Slunce) za stejný čas jsou stejně velké.".
Velikost i směr průvodiče se při pohybu planety po trajektorii neustále mění. Průvodič však vždy za stejnou
dobu opíše plochu se stejným obsahem. Tento zákon se někdy nazývá zákon ploch. Planety se v přísluní pohybují nejrychleji,
v odsluní zase nejpomaleji. Trajektorie je rozdělena na zvolený počet úseků (položka body, implicitní hodnota je 40, skutečný časový
interval bodů je v levém horním rohu).
Pokud se kurzorem myši přiblížíte k tomuto bodu, změní se kurzor křížku na šipku s otazníkem. Jestliže kliknete,
vybere se tento bod a zobrazí se úsečka spojující ohnisko F1 a vybraný bod společně s informací (ve spodní části formuláře),
kolik tato úsečka měří v astronomických jednotkách (au), přičemž se zohledňuje poloha planetky v prostoru.
Když vyberete stejným způsobem další bod, dokreslí se trojúhelník a vypočítá jeho plocha pomocí Heronova vzorce (známe délky všech stran).
Pomocí Esc (nebo vybráním dalšího bodu) se označení zruší.
Výpočet plochy nezohledňuje zakřivení trajektorie planetky, pokud je časový interval příliš velký, může dojít k nepřesnostem.
Body lze vybrat i mimo trajektorii planetky, v tomto případě již není zohledněn sklon dráhy k ekliptice (poloha objektu v prostoru).
Vzdálenosti se pak počítají jen v rovině ekliptiky.
- Třetí Keplerův zákon
"Poměr druhých mocnin oběžných dob dvou planet je stejný jako poměr
třetích mocnin jejich hlavních poloos."
Hodnotu velké poloosy a můžeme vypočítat jako polovinu součtu vzdáleností (průvodiče r) objektu v přísluní a odsluní. Hodnoty
těchto vzdáleností najdete na přímce apsid.
![Vzorec 1 - a=1/2*[r(peri)+r(apo)]](/obr/planety/planetky/vzorec1.gif)
Vypočítanou velikost a lze zkontrolovat z výše uvedené tabulky, kde se nachází dráhové elementy planetky.
Z velikost velké poloosy je pak pomocí třetího Keplerova zákona vypočítána oběžná doba planetky zobrazená
v levém horním rohu obrázku.