Vlastnosti bílých trpaslíků

Hmotnost

Hmotnost hvězdy je nejvýznamnější charakteristikou každé hvězdy, jež určuje nejen délku jejího života, ale i například zánik. U bílých trpaslíků tomu není jinak.

Chandrasekharova teorie

V kapitole věnované historii jsem zmínil, že Subrahmanyan Chandrasekhar dospěl ve svých výpočtech k tomu, že limitní hmotností bílých trpaslíků je rovna 1,44 M_S. Také jsem uvedl myšlenkový postup, který ho k tomuto výsledku dovedl, a nastínil jsem, jaká úskalí musel Chandrasekhar překonat. Chandrasekharova teorie není matematicky jednoduchá, nicméně si ji můžeme za určitých podmínek přiblížit. Předpokládejme proto zjednodušený tvar rovnice hydrostatické rovnováhy, do níž dosadíme průměrné hodnoty. Tedy:

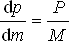(4.1)

kde P je průměrný tlak, který můžeme nahradit v našem zjednodušení tlakem degenerovaného plynu s průměrnou hustotou ρ. M značí hmotnost hvězdy.

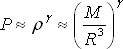(4.2)

γ je adiabatický index, R značí poloměr hvězdy.

V rovnici (4.1) máme tedy na pravé straně gravitační člen f_g a na levé straně tlakový člen f_p .

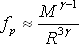(4.3)

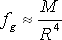(4.4)

Má-li nastat v bílém trpaslíkovi rovnovážný stav, musí být poměr těchto činitelů roven jedné.

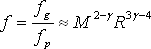(4.5)

Za γ dosadíme adiabatický index roven 5/3 (pro nerelativistický degenerovaný plyn), respektive 4/3 (pro relativistický degenerovaný plyn). Výsledkem bude závislost hmotnosti M na poloměru R.

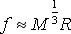(4.6)

pro γ rovno 5/3 a

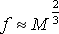(4.7)

pro γ rovno 4/3.

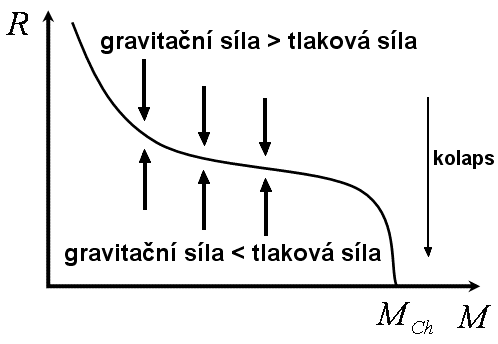
Předpokládejme, že máme bílého trpaslíka o hmotnosti M < M_Ch (M_Ch značí kritickou hmotnost – Chandrasekharovu mez) z nerelativistického degenerovaného plynu, jehož γ = 5/3. Rovnovážný stav nastává, je-li  f = 1. K tomu stačí přizpůsobit poloměr R. V případě, kdy M > M_Ch a tím pádem je i  f > 1, gravitace převáží tlakovou sílu degenerovaného plynu a poloměr R se zmenší natolik, aby byla splněna podmínka  f = 1 (viz 4.6).

Nicméně, máme-li trpaslíka složeného z relativistického degenerovaného plynu, kde γ = 4/3, pak hodnota  f je na poloměru R nezávislá. Rovnováha tudíž nastane pouze tehdy, když hmotnost M dosahuje určité hodnoty (M = M_Ch). Bude-li M < M_Ch, pak  f < 1 a tlak degenerovaného plynu donutí trpaslíka expandovat. Tím se i adiabatický index γ zvýší nad kritické 4/3. Na druhou stranu, bude-li hmotnost trpaslíka M > M_Ch a tím i  f > 1, gravitace trpaslíka stlačí. Z rovnice (4.7) je patrné, že nezávislost na poloměru R způsobí kolaps – rovnováha nebude nikdy ustálena

Předešlý myšlenkový postup tedy můžeme uzavřít s tím, že M_Ch je kritická hmotnost pro nastolení rovnovážného stavu (viz graf níže).

Závislost poloměru hvězdy na její hmotnosti

Rozložení hmoty a skutečná hmotnost bílých trpaslíků ve vesmíru

Na vzorku bílých trpaslíků spektroskopických typů DA a DB si ukážeme, jak je to ve vesmíru s jejich skutečnými hmotnostmi.

Z měření se ukázalo, že typ DA má velmi ostrý pík kolem hodnoty 0,6 M_S. Průměrná hmotnost tak činí M_DA = 0,590 M_S ± 0,134 M_S.

Rozložení hmotnosti bílých trpaslíků typu DA
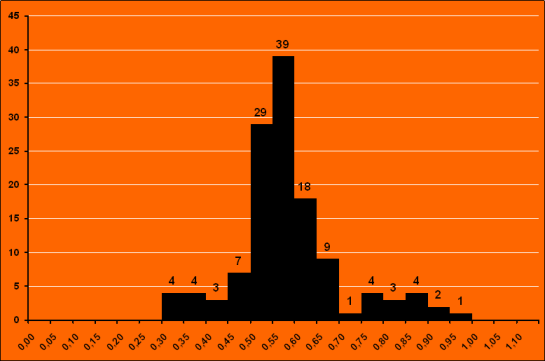
Zdroj dat: Encyclopedia Of Astronomy and Astrophysics, Nature: 2001.

Na levé straně od ostrého píku se nacházejí málo hmotní bílí trpaslíci s heliovým jádrem, kteří pravděpodobně vznikli vývojem v binárních systémech evolucí v těsných vazbách s druhou složkou. Na pravé straně se pak nacházejí velmi hmotní bílí trpaslíci, kteří pravděpodobně vznikli také v binárních systémech, avšak sloučením obou složek. Nicméně i v tomto případě existují výjimky – například hmotnost Siria B dosahuje hodnoty 1,05 M_S.

Typ DB vykazuje téměř stejnou průměrnou hmotnost, kdy M_DB = 0,585 M_S ± 0,063 M_S.

Rozložení hmotnosti bílých trpaslíků typu DA
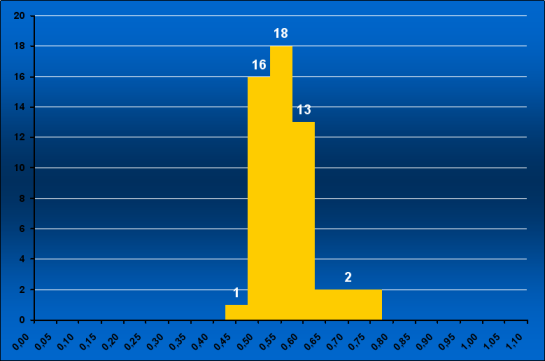
Zdroj dat: Encyclopedia Of Astronomy and Astrophysics, Nature: 2001.

Všimněme si však, že u typu DB téměř chybí levá a pravá strana v grafu. Astronomové se domnívají, že velmi hmotní a málo hmotní bílí trpaslíci nemají v typu DB žádné zastoupení (proto tak malá odchylka v průměrné hmotnosti).

Složení a hustota

Z empirických pozorování je patrné, že bílí trpaslíci obsahují zbytkové množství helia a vodíku. Vezmeme-li v potaz předchozí termojaderné reakce a mechanismus tzv. gravitačního usazování, kdy těžší prvky klesají ke středu, představa o struktuře průměrně hmotného bílého trpaslíka (M ~ 0,6 M_S) vypadá asi následovně:

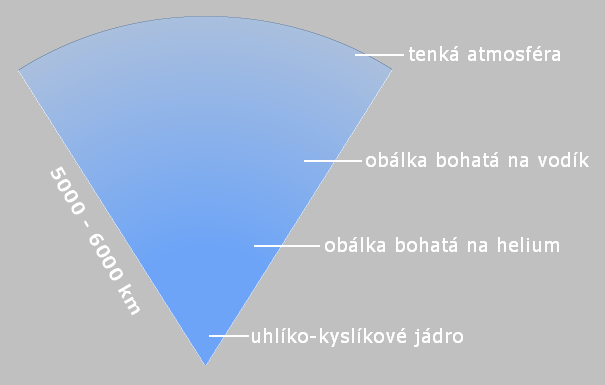
Střed vyplňuje uhlíko-kyslíkové jádro obsahující 99 % hmotnosti, které je obklopeno obálkou bohatou na helium. Nad ní leží obálka bohatá na vodík. Tloušťka těchto obálek či jádra není známá, vždy závisí na způsobu, kterým se trpaslík zrodil. Teoreticky je však spočítáno, že hmotnost helia a vodíku, které zbude po termonukleárních reakcích, dosahuje jen 1/100, respektive 1/10 000 hmotnosti původní.

Povrch je zahalen tenkou atmosférou, o níž z předchozí části věnované spektroskopickým typům již víme, že nejvýznamnějšími prvky tvořícími atmosféru bílých trpaslíků jsou vodík (typ DA) a helium (typy DO, DB, DC, DQ a DZ). Mluvíme tedy o typech atmosfér DA a non-DA. Takto přesná klasifikace je možná právě díky zmiňovanému gravitačnímu usazování (prvky těžší než ty dominantní jsou gravitačně „tlačeny“ k povrchu, a tak prakticky neovlivňují vlastnosti atmosféry). Díky velmi vysoké opacitě hmoty, z níž je bílý trpaslík složen, je atmosféra prakticky jediným zdrojem elektromagnetického záření, a tím i zdrojem informací.

Pomyslný řez bílým trpaslíkem

Průměrná hustota objektu, jakým je bílý trpaslík, dosahuje hodnot ~10⁹ kg·m^–3, což je pro představu milionkrát větší hustota, než je hustota Slunce.

Rotace

Další zajímavou vlastností bílých trpaslíků je jejich pomalá rotace. Pomalá proto, že rotují pomaleji, než by měli v případě, že by se zachovala jejich úhlová hybnost z předchozího vývoje. Z pozorování je patrné, že hvězda musela ztratit podstatnou část své úhlové hybnosti ještě předtím, než se stala bílým trpaslíkem. Protože neexistuje žádný model, který by toto vysvětloval, soustředí se současné pokusy o interpretaci na fakt, že většina hvězd nutně ztratí velké množství hmoty a pak teprve zanikne v podobě trpaslíka.

Povrchová gravitace a zářivý výkon

Spektroskopickou analýzou dokážeme určit velikost povrchového gravitačního zrychlení, protože intenzita a šířka různých spektrálních čar je ovlivňována hustotou atmosféry. K výpočtu se pak používá známý vzorec

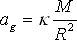(4.8)

κ značí gravitační konstantu, M je hmotnost bílého trpaslíka a R je jeho poloměr.

Hodnoty se však zapisují pomocí logaritmu o základu 10 – log a_g. Průměrné gravitační zrychlení na povrchu bílých trpaslíků dosahuje hodnoty ~10⁶ m·s^–2 (log a_g ~ 8 (cm·s^–2)). To můžeme srovnat se Sluncem – 10^2,4 m·s^–2 (log a_g ~ 2,4 (cm·s^–2)) – což plně koresponduje s průměrnou hmotností bílých trpaslíků.

Rozsah zářivého výkonu kopíruje široké rozpětí pozorovaných teplot, neboť magnituda se pohybuje v sedmi řádech. Nejslaběji zářící známý bílý trpaslík dosahuje pouze zářivého výkonu L ~ 10^-4,3 L_S, zatímco na opačné straně intervalu se nacházejí trpaslíci vstupující do fáze ochlazování s L ~ (10² – 10³) L_S.