fyzikální vlastnosti černých děr
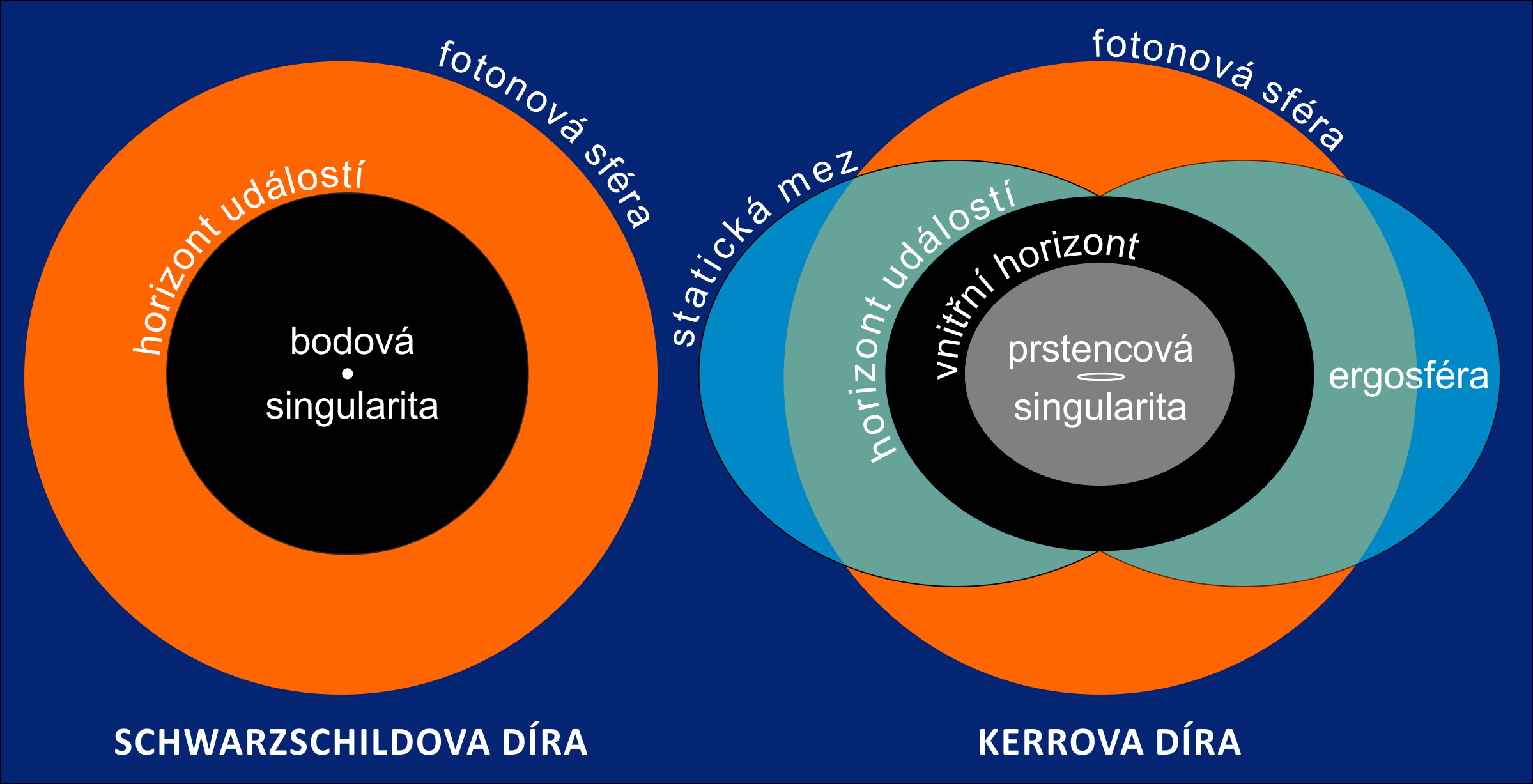
vnitřní a vnější struktura černé díry
Hlavní charakteristiky Schwarzschildovy (nerotující) černé díry
Horizont událostí
- Horizont událostí tvoří kuloplochu kolem černé díry, kde úniková rychlost dosahuje hodnoty rychlosti světla ve vakuu. To znamená, že světlo nemůže tuto oblast opustit, ale zároveň není přímo pohlceno, ale sebemenší narušení vede k nestabilitě takového obíhání fotonů a případném spirálovitém pádu do černé díry. Tato sféra je zásadní v popisu černých děr, protože veškeré hmotné či nehmotné informace co se dostanou za horizont událostí jsou již navždy ztraceny a už nikdy se nedostanou ven.
- Vyjímku tvoří kvantované páry částic a antičástic, které se tvoří a spolu i zanikají v blízkosti horizontu událostí a hrají důležitou roli ve vypařování černých děr.
- Velikost Schwarzschildova poloměru u takto nerotující černé díry je rovna právě horizontu událostí.
- Pokud by se taková černá díra nacházela před jasně zářícím objektem, například mlhovinou, vzdálený pozorovatel by v jejím místě viděl tmavý disk. Vzhledem k tomu, že z oblasti horizontu událostí nemůže uniknout žádná informace, není možné pozorovat, co se děje uvnitř. Veškeré poznatky o vnitřní struktuře černé díry proto vycházejí výhradně z matematických modelů a teoretických výpočtů.
Singularita
- Singularita je podle obecné teorie relativity bod ve kterém je soustředěna veškerá hmotnost černé díry a je bezrozměrný, neboli nemá žádný objem. Objekt s nenulovou hmotností a nulovým objemem by měl nekonečnou hustotu, což by vedlo k nekonečné intenzitě gravitačního pole na jeho „povrchu“ a k nekonečnému zakřivení časoprostoru.
- Pád jakéhokoliv tělesa za horizont událostí způsobí, že dosáhnutí singularity se objeví v každé z jeho pozorovatelných budoucností, která se týká toho konkrétního tělesa. Jinak řečeno vše co spadne do černé díry se vždy a pouze bude pohybovat k singularitě.
- Důležité je zmínit, že obecná teorie relativity nepřipouští výskyt samotných „nahých“ singularit, které nejsou zaobalené horizontem událostí. Tím pádem je studium singularit velmi obtížné právě kvůli horizontu událostí.
- Kvantová teorie však nepřipouští existenci objektu s nulovými rozměry ve všech směrech. Singularita tedy ve skutečnosti nemusí mít nulový objem, ale spíše představuje hmotu stlačenou do nejmenší možné velikosti.
- Jediná teorie, která nám hraje do karet je teorie superstrun, avšak ta se také rozporuje s objektem o nulovém objemu.
Fotosféra
- U nerotující černé díry má hranice fotosféry nulovou tloušťku a je ve vzdálenosti. Fotony pohybující se po tečně k fotosféře budou nuceny obíhat černou díru po kružnici, kde však nezůstanou příliš dlouhou dobu. Fotony jednak interagují s hmotou padající do černé díry, nebo díky vysoké rychlosti, kterou mají, fluktuují kolem dokonale kruhové fotosféry. To vede buď k jejich pohlcení, nebo opuštění černé díry.
Hlavní charakteristiky rotující černé díry
Akreční disk
- Mimo jiné se kolem černé díry generuje kolosální disk prachu a plynu, který se ve vnitřních oblastech proměňuje na horké plazma. Tato část má velmi vysokou teplotu a výrazně září v tepelném i viditelném spektru. Ta nejvnitřnější oblast akrečního disku se nazývá ISCO, což je poslední stabilní orbita plynu a prachu.
- Pohybující se plazma je vždy doprovázeno impozantním magnetickým polem. To je právě zodpovědné za synchrotronní záření elektronů a také za enormní výtrysky tvořené zkroucenými magnetickými siločarami. Výtrysky se nachází ve směru rotační osy černé díry a mnohdy přesahují velikostně rozměry galaxií. Na koncích výtrysku se energie částic začne pomalu vytrácet a tím vznikají rádiové laloky, které jsou velmi charakteristické pro černou díru a tím je můžeme snadněji pozorovat.
- Podrobnosti obsaženy v kapitole Binární a milisekundové pulsary.
Statická mez
- Rotující černá díra strhává časoprostor ve svém okolí a nutí ho rotovat spolu s ní. Statická mez je pak mez, na níž je časoprostor strháván právě rychlostí světla. Foton se tedy na této mezi nemůže pohybovat proti směru rotace černé díry.
Ergosféra
- Ergosféra je prostor mezi poloměrem horizontu událostí a statickou mezí. Název pochází z řeckého slova „ergo“, což znamená v překladu práce. Částice vlétající do ergosféry totiž mohou tuto zónu opustit s vyšší energií, než do ní vlétly a tak černá díra koná práci na úkor svého momentu hybnosti. Tím se její rotace zpomaluje a plocha ergosféry zmenšuje.
Vnější a vnitřní horizont událostí
- Vnější horizont událostí je nejdůležitější hranicí černé díry. Je to hranice, za kterou se žádná informace ani hmota nemůže dostat zpět – cokoliv, co ji překročí, je nevratně pohlceno černou dírou. Důležité je zmínit, že čím rychleji černá díra rotuje, tím je horizont událostí menší.
- Vnitřní horizont událostí funguje jako taková hranice kauzality, kde se mění vlastnosti prostoročasu. Časoprostor přestává být předvídatelný a běžné fyzikální zákony selhávají. Hypoteticky společně s kerrovou singularitou mohou tyto dvě struktury vést právě k cestování prostorem do jiných vesmírů. Tato myšlenka je hodně hypotetická, ale mohla by být jedno z řešení toho, kam černá díra vede.
Kerrova singularita
- Jak již bylo uvedeno, singularita nerotující černé díry je bodová, tedy má nulový objem. Situace se však mění v případě rotující černé díry, která má nenulový úhlový moment hybnosti. V tomto případě se singularita transformuje do podoby prstence, známého jako prstencová singularita.
- Tento prstenec sice má nulovou tloušťku, ale jeho poloměr je nenulový, což znamená, že se již nejedná o bod, ale o strukturu s určitou rozlohou v prostoru.
- Přítomnost prstencovivé singularity otevírá teoretickou možnost existence průchodu skrze černou díru, tzv. červí díry, a potenciálně i cestování mezi různými oblastmi časoprostoru, i když realita takových konceptů zůstává nejasná.
no hair teorém
„No hair“ teorém („černá díra nemá vlasy“) poprvé zformulovali Brandon Carter, Werner Israel, Ivor Robinson a Stephen Hawking a název vymyslel (opět) John Wheeler. Tato teorie postuluje, že si všechny černé díry při svém vzniku ponechávají informaci pouze o své hmotnosti, momentu hybnosti a elektrickém náboji. Všechny ostatní vlastnosti hmoty mizí průchodem horizontu událostí černé díry.
Platí:
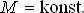 |
(15.1) |
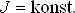 |
(15.2) |
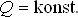 |
(15.3) |
M značí hmotnost černé díry, J je moment hybnosti a Q elektrický náboj černé díry.
Na základě J a Q (žádná černá díra nemá nulovou hmotnost) pak dělíme černé díry následovně:
| Název | Charakteristika | Poznámka | ||
| Schwarzschildovy černé díry |
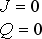 |
nejjednodušší model – předpokládá zhroucení dokonale symetricky kulové hvězdy | ||
| Kerrovy černé díry |
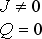 |
výsledek kolapsu rotujících nenabitých těles | ||
| Reisnerovy-Nordstromovy černé díry |
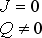 |
mají nulový moment hybnosti a nenulový elektrický náboj – přírodě se s největší pravděpodobností nevyskytují | ||
| Kerrovy-Newmanovy černé díry |
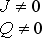 |
obecné řešení černých děr – popisuje většinu v přírodě vzniklých černých děr | ||
Když černé díry ztrácejí informace – záhada, která vědce trápí
Jenže právě tohle tvrzení způsobilo velkou hádku mezi vědci – říká se tomu paradox informace. Podle kvantové fyziky se totiž informace nikdy nemůže úplně ztratit. Když spálíme knihu, zůstane energie a částice, ale informace o tom, co v ní bylo, existuje v jiných formách.
Ale u černých děr to vypadá, že informace, která do nich spadne, zmizí navždy, protože se zvenčí už nikdy nedostane ven. To je v rozporu s tím, co říká kvantová mechanika. A právě tento rozpor je velkým problémem pro fyziky:
Má pravdu Einstein a teorie relativity, nebo kvantová fyzika?
Někteří vědci dnes věří, že černé díry možná přece jen „nějakou paměť“ mají, třeba v oblasti těsně kolem horizontu událostí. Jiní se domnívají, že informace je ukryta v Hawkingově záření, které černé díry velmi pomalu vyzařují.
Tahle záhada ještě není vyřešená, ale právě díky ní dnes fyzici propojují dvě největší teorie: kvantovou mechaniku a obecnou relativitu – a doufají, že je jednoho dne spojí do jedné teorie všeho.
Jak poznáme, že se černá díra točí? Pomocí světla z okolí
I když černou díru nevidíme přímo, dokážeme se o ní hodně dozvědět z toho, jak se chová hmota okolo ní. Například plyn, který do ní padá, se při tom silně zahřívá a začne zářit – zejména v rentgenovém oboru. Tento plyn tvoří tzv. akreční disk, který se točí okolo černé díry jako vír.
Když se na tohle záření podíváme pomocí speciálních přístrojů (spektrometrů), uvidíme, že některé barvy světla se posouvají – podobně jako když se mění zvuk sanitky, která se k nám blíží a pak odjíždí. Tento efekt se nazývá Dopplerův jev. Pokud je část disku blíž k nám, světlo se posune do modra, pokud se vzdaluje, posune se do červena.
Z těchto spektrálních čar můžeme zjistit, jak rychle se disk točí, a tím i to, jestli se černá díra otáčí a jak moc. Vědci tak dokáží měřit i spin černé díry, což je jeden z těch tří „vlasů“, které podle No hair teorému může mít.
entropie černých děr a hawkingovo záření
Entropie černých děr
Černé díry před nás staví zajímavou otázku. Co se děje s látkou (informací), která spadne do černé díry? Podle no-hair teorému stačí k úplnému fyzikálnímu popisu černé díry pouze tři veličiny – její hmotnost, moment úhlové hybnosti a elektrický náboj. Pro úplný popis fyzikálního systému je ovšem nutno určit i entropii, která je mírou neuspořádanosti systému.
Kdyby se entropie při pádu do černé díry „ztrácela“, byl by tím porušen druhý termodynamický zákon, který říká, že entropie v uzavřeném systému (v našem případě můžeme uvažovat vesmír jako uzavřený fyzikální systém, jež nelze opustit vždy roste.
V roce 1972 Stephen Hawking dokázal, že se plocha horizontu událostí nemůže zmenšit. Z tohoto závěru pak Jacob Beckenstein usoudil, že taková plocha reprezentuje entropii černé díry a tím nedochází k porušení druhého termodynamického zákona.
Pro obrázek platí:
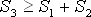 |
(17.1) |
Tento poznatek s sebou ale přinesl další problém. Pokud má černá díra určitou míru entropie, musí mít i svoji teplotu. A „zahřátá“ tělesa jsou nucena zářit, což je v rozporu s klasickým popisem černé díry, že z černé díry nemůže unikat žádná informace.
Fluktuace vakua
Ve vakuu probíhá ve velmi krátkých časových periodách neustálé vytváření a zanikání virtuálních částic, což jsou páry „částice–antičástice“. Tento jev je možný díky Heisenbergově relaci neurčitosti. Ta říká, že pro současné měření polohy x a hybnosti částice p nemůže být součin neurčitostí v určení polohy Δx a hybnosti Δp částice menší než určitá hodnota, která je úměrná Planckově konstantě h. Tento princip v důsledku umožňuje na mikroúrovni porušovat zákon zachování energie a to takovým způsobem, že součin velikosti tohoto narušení a doby, po kterou trvá, je menší než Planckova konstanta. Výsledkem je pak fluktuace energie v podobě zmiňovaného vzniku a zániku virtuálních částic.
(Převzato z hp.ujf.cas.cz)
Hawkingovo záření a vypařování černých děr
Představme si, že dojde ke vzniku virtuální částice v blízkosti horizontu událostí černé díry. V tomto místě je velmi velká šance, že jedna částice z virtuálního páru spadne pod horizont událostí a není schopna zpětně anihilovat s příslušnou antičásticí. Z virtuální částice se stává částice reálná a ta se může vzdálit do „bezpečné“ vzdálenosti od černé díry. Pro vzdáleného pozorovatele tedy černá díra září a aby byl zachován zákon zachování energie, musí černá díra „uhradit“ energii potřebnou ke vzniku reálné částice na úkor své vlastní energie, čímž se zmenší.
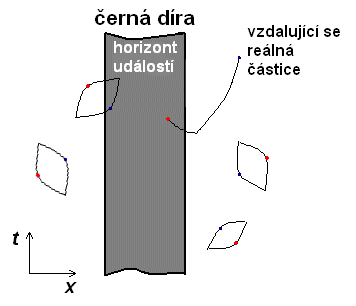
(zdroj obrázku: nrumiano.free.fr)
Spektrum Hawkingova záření je shodné se spektrem záření absolutně černého tělesa a jeho maximální vlnová délka dosahuje hodnoty Schwarzchildova poloměru.
Významným rozdílem mezi Hawkingovým zářením a zářením absolutně černého tělesa (AČT) je ten, že záření AČT má v přírodě statistický charakter a Planckovu vyzařovacímu zákonu odpovídá pouze jeho průměrná hodnota. Hawkingovo záření odpovídá zmíněnému zákonu přesně. Záření AČT tedy obsahuje informace o tělese, které ho vyzářilo, kdežto u Hawkingova záření tomu tak není. To závisí pouze na hmotnosti černé díry, její úhlovém momentu hybnosti a elektrickém náboji.
Platí, že čím větší hmotnost černé díry, tím menší je její teplota. Například černá díra o hmotnosti 6 MS má teplotu K. Intenzita vyzařování tedy závisí na hmotnosti (ploše horizontu událostí). Černá díra s menší hmotností se bude „vypařovat“ rychleji, neboť v jejím případě virtuální částice urazí menší vzdálenost při přeměně na částici reálnou. Černá díra o hmotnosti 6 MS se bude vypařovat 2·1068 let, což je doba, která činí Hawkingovo záření absolutně neměřitelným.
Laboratorní simulace černých děr: Jak vědci testují Hawkingovo záření
Přímé pozorování Hawkingova záření z astrofyzikálních černých děr je mimořádně obtížné, protože jejich teplota je nižší než teplota kosmického mikrovlnného pozadí. Proto vědci hledají alternativní způsoby, jak tento jev ověřit. Jedním z přístupů je vytváření tzv. analogů černých děr v laboratorních podmínkách. (Převzato z Matfyz.cz)
Akustické černé díry: V roce 2016 izraelský fyzik Jeff Steinhauer vytvořil v laboratoři akustickou černou díru pomocí Bose-Einsteinova kondenzátu ultrachladných atomů rubidia-87. V tomto prostředí se mu podařilo pozorovat kvantově provázané páry fononů, které jsou považovány za analogii Hawkingova záření. Tento experiment byl významným krokem k experimentálnímu ověření teoretických předpovědí. (Převzato z Sciencemag.cz+3Osel.cz+3m.techfocus.cz+3)
Optické analogy: Další skupiny vědců, například z Weizmannova institutu v Izraeli, využívají optická vlákna k simulaci černých děr. V těchto experimentech se vytvářejí podmínky, které umožňují pozorovat jevy podobné Hawkingovu záření, například prostřednictvím změn indexu lomu v optickém médiu.
(Převzato z VĚDÁTOR+1Matfyz.cz+1)
Tyto laboratorní simulace poskytují cenné poznatky o kvantových aspektech černých děr a přispívají k lepšímu pochopení Hawkingova záření. Přestože se nejedná o přímé pozorování astrofyzikálních černých děr, tyto experimenty představují důležitý krok k ověření teoretických modelů a prohloubení našeho porozumění kvantové gravitaci.