Vzdálenost a hmotnost dvojhvězdy. Dynamická paralaxa. Vzdálenosti složek
Pokud známe paralaxu dvojhvězdy π, respektive její vzdálenost r, lze pro velkou poloosu trajektorie a psát:
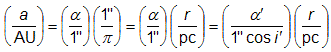 .
.
Pomocí pozorované oběžné periody P v rocích a vypočtené velikosti velké poloosy a v pc lze vypočítat celkovou hmotnost soustavy M. Běžně však vzdálenost dvojhvězdy neznáme, můžeme ji však odhadnout metodou stanovení tzv. dynamické paralaxy. Postup jejího stanovení je iterativní.
Sestává z těchto kroků:
- v prvním kroku předpokládáme, že pro celkovou hmotnost soustavy platí
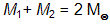 . Z pozorované oběžné periody P a předpokládané hmotnosti soustavy vypočteme odpovídající velkou poloosu soustavy
a1. Pomocí pozorované úhlové velikosti velké poloosy α lze pak vypočítat první odhad vzdálenosti soustavy
r1.
. Z pozorované oběžné periody P a předpokládané hmotnosti soustavy vypočteme odpovídající velkou poloosu soustavy
a1. Pomocí pozorované úhlové velikosti velké poloosy α lze pak vypočítat první odhad vzdálenosti soustavy
r1. - z pozorovaných hvězdných velikostí hi obou složek lze také odhadnout odpovídající absolutní hvězdné velikosti Hi podle vztahu:
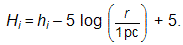 .
. - nyní z tabelovaného vztahu mezi absolutní hvězdnou velikostí a hmotností (důsledek vztahu hmotnost–zářivý výkon) H(M) najdeme odpovídající hmotnosti pro každou ze složek dvojhvězdy a sečteme je. Dostaneme tak další odhad pro celkovou hmotnost soustavy M.
- z pozorované oběžné periody P a nově odhadnuté hmotnosti soustavy vypočteme odpovídající velkou poloosu soustavy a. Pomocí pozorované úhlové velikosti velké osy α lze pak vypočítat druhý odhad vzdálenosti soustavy r2.
- nyní se opět vrátíme na bod b) a pokračujeme v dalším kole iterací. Činíme tak, dokud výsledek nedospěje ke konečné hodnotě vzdálenosti. Zkušenost ukazuje, že obvykle vystačíme s třemi iteračními kolečky.
Převrácená hodnota takto nalezené vzdálenosti se nazývá dynamická paralaxa. Touto metodou byla odhadnuta vzdálenost velkého množství vizuálních dvojhvězd, což umožnilo dobře zmapovat řadu zajímavých hvězdných systémů i jednotlivých dvojic. Metoda dynamické paralaxy je cenná hlavně tím, že její spolehlivost, na rozdíl od paralaxy trigonometrické, nezávisí na vzdálenosti. Omezení spočívá v různé míře použitelnosti vztahu mezi absolutní hvězdnou velikostí a hmotností. Negativně se zde též projevuje vliv extinkce, jejíž velikost touto metodou nelze odhadnout.
Občas stojíme před jiným úkolem - známe oběžnou periodu P ve dnech a podle spektrálního typu můžeme odhadnout i hmotnost primární složky M1. Nás teď zajímá, jak jsou od sebe složky v prostoru vzdáleny, čili hledáme velkou poloosu dráhy a, vyjádřenou nejlépe v poloměrech slunečních. 3. Keplerův zákon pak nabude této podoby:
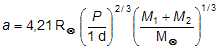 .
.
Na závadu zde ovšem je, že zpravidla neznáme hmotnost sekundární složky. Uvážíme-li ovšem, že poměr hmotností složek M1/M2 by měl ležet v intervalu 0 až 1, pak
obdržíme pro střední vzdálenost složek velmi užitečnou nerovnost: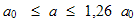 , kde a0 odpovídá vzdálenosti složky se zanedbatelnou hmotností:
, kde a0 odpovídá vzdálenosti složky se zanedbatelnou hmotností:
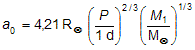 .
.