Zákrytové dvojhvězdy

Objev zákrytových dvojhvězd

Na přelomu let 1782-83 John Goodricke (1764-86) prokázal, že jedna z prvních objevených proměnných hvězd – Algol mění svou jasnost pravidelně, a to s periodou necelých tří dní. Týž Goodricke správně vysvětlil jeho světelné změny tím, že jde o dvojhvězdu, jejíž složky se při oběhu vzájemně zakrývají. Největší autorita té doby, William Herschel, naproti tomu soudil, že jde o projev temných skvrn na rotující hvězdě. V té době v existenci fyzických dvojhvězd ještě nevěřil. V roce 1880 Edward C. Pickering oprášil již skoro sto let starou Goodrickovu domněnku o dvojhvězdné povaze proměnné hvězdy a dokázal, že výborně odpovídá pozorování. Z tvaru světelné křivky odvodil i relativní rozměry obou složek. Osm let nato zjistil Hermann Vogel, že Algol je jednosložkovou spektroskopickou dvojhvězdou, jejíž křivka radiální rychlosti přesně odpovídá dvojhvězdnému modelu. Bezpečně tak byl kombinací fotometrických a spektroskopických pozorování prokázán mechanismus proměnnost i tzv. zákrytových dvojhvězd. O definitivní potvrzení domněnky se zasloužil nedávný výzkum, kdy spojením několika radioteleskopů rozmístěných po celé Severní Americe byl vytvořen jedinečný radiový interferometr s dlouhou základnou (VLBI). Výsledná rozlišovací schopnost tohoto instrumentu byla 0,0005“. Pozorování radiového zdroje v místě zákrytové dvojhvězdy ve shodě s očekáváním prokázala, že zdroj kmitá v severojižním směru tam a zpět v rámci úsečky o délce 4 tisícin úhlové vteřiny. Tento pohyb opakovaný s periodou 2,87 dne odpovídá oběžnému pohybu Algolu B. Zcela nová tu ovšem je informace o orientaci oběžné trajektorie dvojhvězdy v prostoru, kterou nebylo možné získat ani rozborem světelných změn zákrytové soustavy, ani ze spektroskopických výzkumů.

Podmínky zákrytů. Astrofyzikální využití zákrytových dvojhvězd

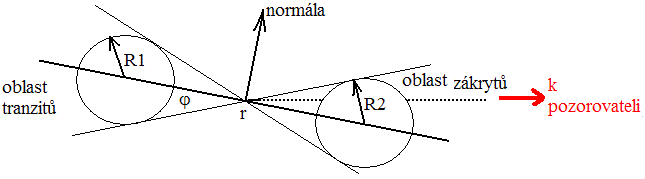
K zákrytům složek dochází v případě, kdy rovina oběžné trajektorie dvojhvězdy prochází nedaleko od pozorovatele: i~90°. Vše dále řešíme pro zjednodušený případ dvojhvězdy, kde se složky ve tvaru koule o poloměrech R₁ a R₂ pohybují po kruhových drahách ve vzájemné vzdálenosti složek r. Zákryty budeme pozorovat v tom případě, kdy bude sklon trajektorie i větší než 90° (φ₀). Přitom lze φ₀ vypočítat ze vztahu:

.

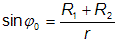Je zřejmé, že k zákrytům bude docházet s nemalou pravděpodobností, a to zejména v případě soustav, které jsou relativně těsné. Za těchto okolností ovšem nebude tak zcela splněna podmínka kulového tvaru hvězdy, nicméně jako odhad vypočtená relace dobře postačí. Dojde-li k vzájemným zákrytům složek dvojhvězdy, získáme dodatečnou informaci o geometrii soustavy z rozboru pozorované světelné křivky. Z ní lze především určit:

• sklon oběžné trajektorie k pozorovateli i;
• relativní rozměry složek R₁/r, R₂/r;
• při vysoce kvalitních pozorováních lze odvodit i rozložení jasu na hvězdných discích, čili stanovit tzv. okrajové ztemnění (jde o velmi cennou informaci umožňující testovat adekvátnost různých variant modelů hvězdných atmosfér);
• relativní svítivosti (zářivé výkony) obou složek.
  Zkombinujeme-li to s informacemi, které získáme z křivky radiálních rychlostí, lze navíc odvodit:
• lineární vzdálenost složek, a tím i absolutní rozměry složek dvojhvězdy.
  Ze spektra nebo z fotometrie můžeme stanovit efektivní teploty složek dvojhvězdy. Tímto pak lze:
• ze znalosti poloměrů hvězd stanovit zářivé výkony hvězd, jejich absolutní bolometrické hvězdné velikosti;
• ze známých absolutních hvězdných velikostí a pozorovaných hvězdných velikostí pak konečně odvodit i vzdálenost soustavy;

Zákrytových dvojhvězd známe nyní několik tisíc, periody těchto soustav jsou hodiny až desítky dnů, výjimkou jsou zákrytové systémy s orbitální periodou nad jeden rok. Určování elementů trajektorie známých systémů je ještě svízelnější než v případě spektroskopických dvojhvězd, protože zde často bývá k dispozici jen světelná křivka.

Výklad světelné křivky

Na vzhledu světelné křivky se spolupodílí řada okolností, a to:

• geometrie systému, čili sklon trajektorie a relativní velikosti složek;
• rozložení jasu na kotoučích hvězd, čili okrajové ztemnění hvězd, jehož parametry jsou dány stavbou hvězdné atmosféry;
• u těsnějších systémů způsobuje komplikace asféričnost složek, které jsou slapově deformovány, někde i existence společných atmosfér (hvězdy typu W Ursae Majoris) a existence svítící či absorbující látky pocházející z přetoku hmoty mezi složkami;
• u těsných soustav bývá důležitý i rozptyl záření druhé složky v systému.

Vše je velice komplikované, nicméně v současnosti existuje řada spolehlivých výpočetních programů, které jsou schopny tyto informace (v různém stupni spolehlivosti) z analýzy světelné křivky vytěžit. Pro ilustraci si vyberme značně zjednodušený případ, kdy zkoumaná zákrytová soustava sestává ze dvou kulových hvězd o poloměrech R₁ a R₂ obíhajících kolem společného těžiště po kruhové trajektorii ve vzdálenosti r. Úhel sklonu i nechť je přitom přesně 90°, čili v soustavě bude docházet k tzv. centrálním zákrytům. Pro naše úvahy zvolíme větší z hvězd o poloměru R₁ za centrální těleso (na volbě nezáleží) a druhá, menší, bude kolem ní stálou rychlostí obíhat tak, že její střed opíše kolem středu centrální složky kružnici za dobu oběhu P.

Přechod (transit)

Pozorujeme-li soustavu z velké vzdálenosti, vidíme, že k prvnímu kontaktu přecházejícího tělesa s tělesem v pozadí dojde ve chvíli, kdy spojnice ke středu druhé složky bude se směrem k pozorovateli svírat úhel α₁, přičemž platí:

; .

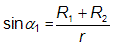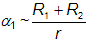Pokud jde o přechod menšího tělesa přes větší, pak budeme sledovat, jak se před kotouč větší složky přesune menší kotouč, který bude systematicky ukusovat stále větší část disku hvězdy v pozadí. Během této fáze částečného zákrytu jasnost soustavy takřka lineárně klesá v důsledku skutečnosti, že vyzařující plocha zakrývané hvězdy se zmenšuje. Ve světelné křivce vidíme pokles, nazývaný sestupná větev minima jasnosti. Rychlý pokles se zastaví v momentu tzv. druhého kontaktu, kdy se na disku centrální hvězdy zobrazí celý kotouč menší složky. V tom okamžiku bude spojnice ke středu druhé složky se směrem k pozorovateli svírat úhel α₂, přičemž platí:

; .

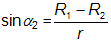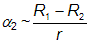Nyní bude kotouč menší složky putovat až do centra kotouče větší složky. V té chvíli nastává střed zákrytu. Vzhledem k tomu, že naprostá většina hvězd jeví nezanedbatelné okrajové ztemnění, bude v této fázi jasnost hvězdy mírně klesat. Na světelné křivce pozorujeme mělké dno – hvězda je v tzv. „zastávce“. Po průchodu centrem celý úkaz symetricky pokračuje. Když se okraj druhé složky zevnitř dotkne okraje hvězdy v  pozadí nastává tzv. třetí kontakt, po němž se začne zmenšovat podíl zakrývané plochy, a to až do momentu čtvrtého kontaktu, který ukončuje vzestupnou větev světelné křivky a celý zákryt. V případě, že lze přistoupit na aproximaci sin α=α délka doby mezi prvním a čtvrtým kontaktem, čili období snížené jasnosti soustavy (doby tzv. minima jasnosti), označovaná zpravidla symbolem D, je dána vztahem:

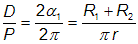
Pro trvání zastávky d v minimu jasnosti dostáváme obdobně:

.

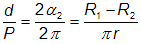Pokud jsme schopni ze světelné křivky odhadnout trvání obou fází, dostaneme tak odhad relativních rozměrů obou složek:

Máme-li to štěstí a známe též křivku radiálních rychlostí obou složek, pak ovšem známe i oběžnou rychlost a tím i absolutní poloměr trajektorie. Pomocí něj vypočítáme absolutní rozměry složek. Nutno upozornit, že toto lze provést, třebaže neznáme vzdálenost soustavy.

Zákryt (okultace)

Přesně po půl periodě dojde k opačné situaci, v popředí bude centrální těleso a za něj se bude skrývat těleso menší. Po prvním kontaktu se část kotouče menší hvězdy skryje za neprůhledným kotoučem centrální hvězdy. Jasnost soustavy bude postupně klesat, a to až do okamžiku druhého kontaktu, kdy kotouč druhé hvězdy zmizí nadobro. Od té chvíle zůstává jasnost soustavy konstantní až do chvíle třetího kontaktu, kdy se na opačné straně centrální hvězdy objeví část kotouče zakrývané hvězdy. Ta se postupně vynoří celá, obě složky se od sebe oddělí v okamžiku tzv. čtvrtého kontaktu. V hlavních rysech je vzhled světelné křivky obdobný jako v případě přechodu (transitu), jen s tím rozdílem, že v zastávce se jasnost systému nemění. Pokud nejsou složky zákrytové dvojhvězdy identické, pozorujeme rozdíly v hloubce obou minim (transit a okultace). Hlubšímu z nich říkáme primární minimum druhému pak minimum sekundární. Pokud je efektivní teplota menší složky nižší než teplota složky větší, pak při transitu nastává hlubší minimum než při okultaci. Pokud je tomu naopak, odpovídá primární minimum zákrytu menšího tělesa. V astrofyzikální praxi se běžně setkáváme s oběma případy. Jsou-li složky dvojhvězdy hvězdami hlavní posloupnosti, pak platí, že hmotnější složka je větší a teplejší než složka méně hmotná.

Vezměme si hypotetický příklad zákrytu dvou hvězd:

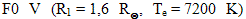a .

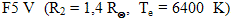Při centrálním transitu při zanedbání vlivu okrajového ztemnění se zvýší bolometrická hvězdná velikost o 0,78 mag, při zákrytu vzroste jen o 0,43 mag. Jiné je to s tzv. klasickými algolidy, kdy se setkáváme s tím, že větší z hvězd je podobr, jenž je zpravidla chladnější a méně hmotný než druhá složka, která bývá hvězdou hlavní posloupnosti. Zvolme si modelový příklad: centrální hvězdou bude podobr o poloměru R₁=5, T_e=4 500 K a druhou složkou hvězda hlavní posloupnosti A0 V (R₂=2,7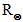, T_e = 9 250 K). Transit se projeví nepatrným zeslabením o 0,05 mag; ale při zákrytu, kdy zmizí primární složka zcela zmizí, vzroste bolometrická hvězdná velikost o 1,99 mag! Je tedy zřejmé, že tzv. algolidy jsou pozorovatelsky zvýhodněny, neboť nabízejí větší pokles jasnosti než soustavy, kde jsou obě složky hvězdami hlavní posloupnosti. Pokud nejsou splněny výše uvedené podmínky (kulové hvězdy, kruhové trajektorie, i = 90°) setkáváme se s komplikovanějšími světelnými křivkami, které se v některých ohledech od našeho idealizovaného případu poněkud liší. Pro pořádek uveďme, že:
Při nenulové excentricitě nebývá sekundární minimum umístěno přesně ve fázi 0,5. Výjimku tvoří situace, kdy je přímka apsid kolineární se směrem k pozorovateli. Na světelné křivce se to ale stejně pozná tak, že pozorovaná zeslabení mají různá trvání.

Při sklonu i 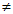90° může jít i v absolutním minimu o částečný zákryt. V tomto případě nenastává v minimu zastávka (d = 0). Z tvaru světelné křivky lze na velikost sklonu i usoudit. Pokud jde o krátkoperiodickou soustavu, jsou složky výrazně slapově deformovány. Během oběhu se mění jejich natočení vůči pozorovateli, a tím i jejich průmět. Důsledkem je fakt, že se jasnost soustavy mění i mezi zákryty. Hvězdy se vzájemně osvětlují – nepřesně se tento efekt, který deformuje a komplikuje pozorované světelné křivky, nazývá efekt odrazu. Nicméně ty nejdůležitější vlivy formující světelnou křivku zde byly zmíněny, ostatní jsou pouze efekty druhého a vyššího řádu.