Hustota pulsarů

Jak již bylo řečeno, z periody pulsarů můžeme odvodit některé vlastnosti. Při výpočtu průměrné hustoty vyjdeme z předpokladu, že k rovnovážnému stavu pulsaru je třeba, aby odstředivé zrychlení na rovníku nepřesáhlo hodnotu zrychlení gravitačního. Uvažujeme ideální pulsar, a tak pro jednoduchost budeme brát průměrné hodnoty všech veličin, zanedbáme i důsledky plynoucí ze stavové rovnice neutronové hmoty.

Má-li pulsar hmotnost M, poloměr R a periodu T, pak pro úhlovou rychlost rovnoměrné rotace platí známý vztah:

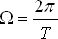(8.1)

tedy:

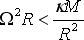(8.2)

κ zde značí gravitační konstantu, M je hmotnost pulsaru a R jeho poloměr.

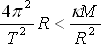(8.3)

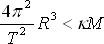(8.4)

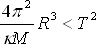(8.5)

Vztah (8.4) vyjadřuje 3. Keplerův zákon.

Jelikož chceme dostat vztah závislý na průměrné hustotě, upravíme (8.5) tak, abychom do něj mohli dosadit z ρ = mV.

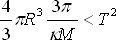(8.6)

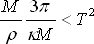(8.7)

Ze vztahu (8.7) pak úpravami dostáváme:

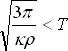(8.8)

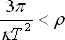(8.9)

Rovnice (8.8) vyjadřuje podmínku minimální doby periody (při poklesu doby periody pod tuto hranici by na rovníku pulsaru převážilo odstředivé zrychlení nad gravitačním, což by vedlo k nestabilitě pulsaru) a vztah (8.9) vyjadřuje podmínku minimální průměrné hustoty.

Hustota pulsarů – příklad

Pulsar PSR J1748-2446ad je nejrychleji rotující pulsar s periodou 0,001 395 954 82 s. Byl objeven Jason W. T. Hesselsovou roku 2004. Aplikujeme-li vztah (8.9) na tento případ, dostáváme:

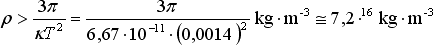(8.10)

Výsledná hustota v řádech 10¹⁶ kg·m^-3 je jedním z důkazů, proč pulsary jsou spíše rychle rotující neutronové hvězdy, než bílí trpaslíci.